Shot down

In 1943, the United States had been a participant in WWII for just over a year. Allied forces were observing many airplanes not returning from missions over Europe. The aircraft that did return were riddled with bullet holes from German anti-aircraft fire. Command wanted to reduce the staggeringly high number of aircraft casualties.

They realized fewer aircraft would be lost over enemy territory if planes had more armour. The challenge was determining the amount and position of additional armour plating to maximize a plane’s protection against deadly enemy flak. Airplanes, however, are the product of engineering trade-off—the more armour you add, the less maneuverability a plane has. You can’t place metal plates along the exterior of an entire airplane like a tank because it will be too heavy to take off. A super safe, but ultimately useless, plane wasn’t what the allies needed.

Seeking an optimal solution

Armouring planes too much is a problem; armouring them too little is also a problem. Somewhere in between, there is an optimal solution. So, where is it best to armour a plane with additional protective layers to maximize its chance of survival without creating a performance limitation or compromising flight capabilities entirely? Where would you put the armour? Have a think before reading on.

To find the answer, the allies began by determining those areas of the aircraft most frequently damaged by enemy fire. Each time a plane returned from a combat mission, the location of the bullet holes was methodically reviewed and recorded. After examining, counting, and cataloging damage to various parts of the airplanes, a fair amount of statistical data was generated.

Evaluating the results showed a clear pattern: the damage was not uniformly distributed across the aircraft. Most damage was concentrated in the wings and fuselages of the planes, with less damage to the engines and cockpits.

Devising a plan

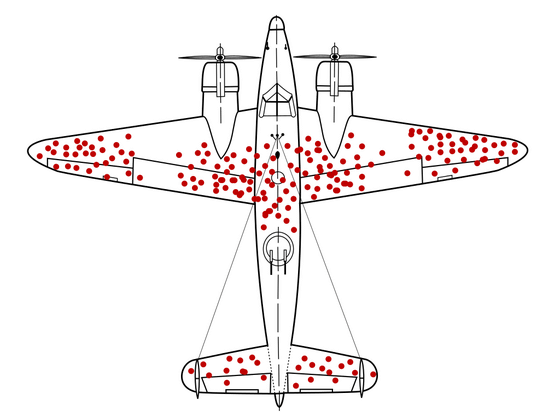
After studying these results, the officers in the field came up with a seemingly rock-solid plan to reduce losses and casualties. The answer to their problem, they reasoned, was clear: add extra armour to the most commonly damaged parts of the planes!

Since the plane’s wings and fuselages attracted the most fire while the engine and cockpit were spared, the solution that would prevent the most damage, and therefore reduce the number of planes shot down, was to concentrate the armour where the planes were being hit the most.

When the obvious fails

Commanders determined they needed to move quickly to bolster the aircraft’s armour in the heavily damaged areas where bullet holes were clustering. They sought to reinforce the wings and fuselages.

But there was a problem: the obvious solution was completely wrong.

Even after putting armour on the areas most susceptible to bullets, the number of planes returning to home base did not improve. It was a disaster.

Recruiting help

Fortunately, the US had a top-secret applied mathematics unit called the Statistical Research Group (SRG). They were tasked with solving various problems that came up during wartime. The SRG was staffed by some of the most distinguished, prominent, and elite American mathematicians and statisticians, including two Nobel Prize winners. In a small office near Columbia University in Manhattan, NY, the US’s best and brightest academic minds and subject matter experts assembled to harness the power of applied statistics for the war effort. SRG’s talent for applying math skills to tricky and virtually incomprehensible problems saved countless lives.

The SRG was challenged to work out the secret of placing armour that offers protection from bullets while ensuring planes were still maneuverable and not unnecessarily heavy. In other words, find a way to keep more allied planes in the air and reduce the number not returning from missions. They were presented with the statistics on planes that had returned safely from combat.

Abraham Wald a key figure in the SRG

Seeing the missing bullet holes

The answer the SRG came up with was surprising. The armour, they argued, shouldn’t go where the bullet holes are. It should go where the bullet holes are not: on the engines and cockpit.

But why would they suggest that when the planes were taking more damage to the wings and fuselages than to their engines and cockpits? It’s because of an assumption that was catastrophically wrong.

The mathematicians quickly saw through the common-sense paradigm and spotted a critical flaw in the analysis. German flak is deadly but not terribly accurate, they pointed out, so hits should presumably be equally distributed across the plane. There should have been holes all over, including on the engine and cockpit portions as well. It was highly unlikely that certain areas would simply be missing bullet strikes. The SRG’s insight was to ask about the missing bullet holes.

The missing bullet holes were on the missing planes—the ones that had been shot down and didn’t return. The areas where the returning planes were unscathed were those areas that, when hit, would cause the plane to crash and be lost. The bullet holes in returning planes did not show where the planes were suffering the most damage; instead, they showed where planes could be shot and take damage.

The holes in returning aircraft were in areas that needed no extra armour.

The solution in the sample set

The planes getting hit in the engines and cockpits were going down and being lost over enemy territory; they never made it back to be analyzed as part of the sample set. The SRG recognized they were analyzing a biased sample that told an incomplete story—it didn’t paint an accurate picture. The sample they were looking at was much different than what randomness would produce; in other words, they could only study the planes that had landed back at base.

The reason aircraft rarely had damage to the engine and cockpit wasn’t because of superior protection to those areas—it’s because those were the most vulnerable areas to enemy fire. Some planes successfully returned because they were damaged in places that could tolerate rounds tearing through them. The undamaged locations were actually the weakest areas.

The SRG’s ingenious deduction led them to recommend placing additional armour on the parts of the plane were there were no bullet holes—exactly the opposite of what the top brass had been doing.

Testing the deduction

The advice was taken, and crews quickly implemented the SRG’s proposed design revisions and reinforced the planes’ engines and cockpits.

The results were stunning. Immediately, planes were safer to fly and ultimately started surviving more hits and making more round trips with fewer fatalities. The analysis proved to be so useful that it continued to influence military plane design and saved countless lives in later conflicts in Korea and Vietnam. The SRG’s insights continue to be useful to this day.

Understanding the counterintuitive

So, why was the counterintuitive answer right?

The SRG was cleverly taking into account a flaw that eluded others faced with the same problem. The flaw would become known as survivorship bias, a classic fallacy so common you will start seeing it everywhere once you understand it.

Survivorship bias is a type of selection bias that focuses on the survivors (or those that remain) when evaluating an event or outcome. In other words, it is the tendency to concentrate on people or statistics that make it past some selection process while overlooking those that did not, typically because they are (and especially in this case) less visible. Survivorship bias leads to making a lot of bad decisions by telling distorted and incomplete stories based on inaccurate information and causes conclusions that are entirely wrong.

This story described a vivid example of survivorship bias because the final sample set excluded the (often invisible) parts of the sample that didn’t survive. In this case, the error was looking only at subjects who had reached a certain point but not looking at those who hadn’t. The SRG’s reasoning and conclusions were based on considering and understanding the scenario and finding another way to look at the challenge to see something concealed in everyone else’s blind spot. Once you understand and follow the logic, the right answer seems as obvious as the biased answer was.

But I’m sure you can imagine how it defied the idea of common sense when the SRG looked at the dilemma and offered an entirely different conclusion.

The takeaway

The US Air Force suffered over 88,000 casualties during WWII and without the SRG’s research this number would undoubtedly have been higher. Of course, the SRG’s contrarian instincts alone didn’t turn the tide and win the war—without brave soldiers and superior equipment things would have been much different—but allied pilots and crew members safely returning from combat were probably thankful for the insights they offered.